Simulado UFF de Matematica | VESTIBULAR
📚 Simulado UFF | Vestibular | cód.8078
Estude com estratégia: o simulado UFF foi criado pensando em você! 📘
🎯 São milhares de simulados para concurso disponíveis para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
🧪 Este Simulado UFF foi elaborado da seguinte forma:
- 📌 Categoria: Vestibular
- 🏛️ Instituição: UFF
- 👔 Cargo: Vestibular
- 📚 Matéria: Matemática
- 🧩 Assuntos do Simulado:
- 🏢 Banca Organizadora: UFF
- ❓ Quantidade de Questões: 17
- ⏱️ Tempo do Simulado: 51 minutos
⚙️ REGRA DO SIMULADO
Este simulado é gratuito 🆓. Basta clicar no botão iniciar abaixo e preencher um breve cadastro para participar do nosso ranking.
📊 No ranking você compara sua nota com outros candidatos e acompanha sua evolução nos estudos.
🚀 Aproveite este simulado UFF e saia na frente na sua preparação!
📖 Questões UFF
Se ainda não estiver pronto para fazer o simulado, treine antes com nossas questões de concursos:
🎥 Vídeo Aula
Confira vídeo aulas no YouTube com foco no concurso UFF. Estude com conteúdo gratuito e atualizado.
📚 Apostila
Encontre apostilas completas e materiais didáticos atualizados para o concurso UFF.
📢 Concursos Abertos para UFF
Veja os concursos abertos da instituição UFF. A lista está sempre atualizada:
🍀 Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z ✅
- #120608
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 16 -

Se a = 0; b = 10; p = 0,1; e sabendo que x(0) = 2 000 e y(0) = 200; então, a distribuição de indivíduos no ano t = 10 é dada por:
- a) x(10) = 20 000 e y(10) = 2 000
- b) x(10) = 2 000 e y(10) = 200
- c) x(10) = 2 00010 e y(10) = 200 10
- d) x(10) = 2 000 1010 e y(10) = 200 10-10
- e) x(10) = 2 000 10-10 e y(10) = 200 1010
- #120609
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 17 -

O intervalo de tempo necessário para que o número de núcleos radioativos seja reduzido à metade é denominado tempo de meia-vida. Pode-se afirmar que o tempo de meia-vida:
- a)

- b) é igual a 1/2
- c) é igual a 2
- d)
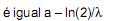
- e)