Simulado Probabilidade para o Enem | ENEM

(1,0) 1 - 

Um aluno de uma escola será escolhido por sorteio para representá-la em uma certa atividade. A escola tem dois turnos. No diurno há 300 alunos, distribuídos em 10 turmas de 30 alunos. No noturno há 240 alunos, distribuídos em 6 turmas de 40 alunos.
Em vez do sorteio direto envolvendo os 540 alunos, foram propostos dois outros métodos de sorteio.
Método I : escolher ao acaso um dos turnos (por exemplo, lançando uma moeda) e, a seguir, sortear um dos alunos do turno escolhido.
Método II: escolher ao acaso uma das 16 turmas (por exemplo, colocando um papel com o número de cada turma em uma urna e sorteando uma delas) e, a seguir, sortear um dos alunos dessa turma. Sobre os métodos I e II de sorteio é correto afirmar:

(1,0) 2 - 

A queima de cana aumenta a concentração de dióxido de carbono e de material particulado na atmosfera, causa alteração do clima e contribui para o aumento de doenças respiratórias. A tabela abaixo apresenta números relativos a pacientes internados em um hospital no período da queima da cana.

Escolhendo-se aleatoriamente um paciente internado nesse hospital por problemas respiratórios causados pelas queimadas, a probabilidade de que ele seja uma criança é igual a

(1,0) 3 - 

O controle de qualidade de uma empresa fabricante de telefones celulares aponta que a probabilidade de um aparelho de determinado modelo apresentar defeito de fabricação é de 0,2%. Se uma loja acaba de vender 4 aparelhos desse modelo para um cliente, qual é a probabilidade de esse cliente sair da loja com exatamente dois aparelhos defeituosos?

(1,0) 4 - 

A população brasileira sabe, pelo menos intuitivamente, que a probabilidade de acertar as seis dezenas da mega sena não é zero, mas é quase. Mesmo assim, milhões de pessoas são atraídas por essa loteria, especialmente quando o prêmio se acumula em valores altos. Até junho de 2009, cada aposta de seis dezenas, pertencentes ao conjunto {01, 02, 03, ..., 59, 60}, custava R$ 1,50.
Disponível em: www.caixa.gov.br. Acesso em: 7 jul. 2009.

Considere que uma pessoa decida apostar exatamente R$ 126,00 e que esteja mais interessada em acertar apenas cinco das seis dezenas da mega sena, justamente pela dificuldade desta última. Nesse caso, é melhor que essa pessoa faça 84 apostas de seis dezenas diferentes, que não tenham cinco números em comum, do que uma única aposta com nove dezenas, porque a probabilidade de acertar a quina no segundo caso em relação ao primeiro é, aproximadamente,

(1,0) 5 - 

Um médico está estudando um novo medicamento que combate um tipo de câncer em estágios avançados. Porém, devido ao forte efeito dos seus componentes, a cada dose administrada há uma chance de 10% de que o paciente sofra algum dos efeitos colaterais observados no estudo, tais como dores de cabeça, vômitos ou mesmo agravamento dos sintomas da doença. O médico oferece tratamentos compostos por 3, 4, 6, 8 ou 10 doses do medicamento, de acordo com o risco que o paciente pretende assumir.

Se um paciente considera aceitável um risco de até 35% de chances de que ocorra algum dos efeitos colaterais durante o tratamento, qual é o maior número admissível de doses para esse paciente?

(1,0) 6 - 

Rafael mora no Centro de uma cidade e decidiu se mudar, por recomendações médicas, para uma das regiões: Rural, Comercial, Residencial Urbano ou Residencial Suburbano. A principal recomendação médica foi com as temperaturas das “ilhas de calor” da região, que deveriam ser inferiores a 31 °C. Tais temperaturas são apresentadas no gráfico:

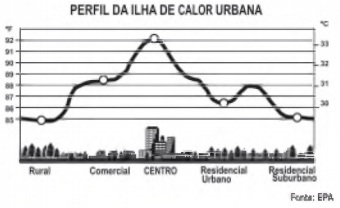
Escolhendo, aleatoriamente, uma das outras regiões para morar, a probabilidade de ele escolher uma região que seja adequada às recomendações médicas é

(1,0) 7 - 

Em um jogo disputado em uma mesa de sinuca, há 16 bolas: 1 branca e 15 coloridas, as quais, de acordo com a coloração, valem de 1 a 15 pontos (um valor para cada bola colorida).

O jogador acerta o taco na bola branca de forma que esta acerte as outras, com o objetivo de acertar duas das quinze bolas em quaisquer caçapas. Os valores dessas duas bolas são somados e devem resultar em um valor escolhido pelo jogador antes do início da jogada.

Arthur, Bernardo e Caio escolhem os números 12, 17 e 22 como sendo resultados de suas respectivas somas.

Com essa escolha, quem tem a maior probabilidade de ganhar o jogo é

(1,0) 8 - 

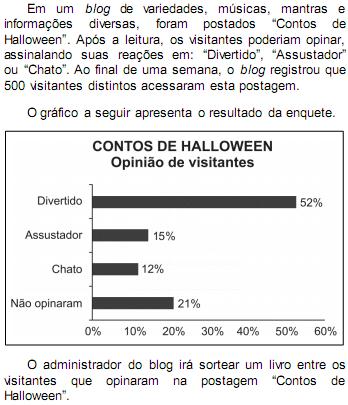
Sabendo que nenhum visitante votou mais de uma vez, a probabilidade de uma pessoa escolhida ao acaso entre as que opinaram ter assinalado que o conto “Contos de Halloween” é “Chato” é mais aproximada por

(1,0) 9 - 

Numa escola com 1 200 alunos foi realizada uma pesquisa sobre o conhecimento desses em duas línguas estrangeiras, inglês e espanhol. Nessa pesquisa constatou-se que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas.
Escolhendo-se um aluno dessa escola ao acaso e sabendo-se que ele não fala inglês, qual a probabilidade de que esse aluno fale espanhol?

(1,0) 10 - 

O psicólogo de uma empresa aplica um teste para analisar a aptidão de um candidato a determinado cargo. O teste consiste em uma série de perguntas cujas respostas devem ser verdadeiro ou falso e termina quando o psicólogo fizer a décima pergunta ou quando o candidato der a segunda resposta errada. Com base em testes anteriores, o psicólogo sabe que a probabilidade de o candidato errar uma resposta é 0,20.

A probabilidade de o teste terminar na quinta pergunta é