Prova Geometria Analítica para o Enem | ENEM

(1,0) 1 - 

A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em torno do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.

Considere que o volume aproximado dessa bola é dado por V = 4ab².

O volume dessa bola, em função apenas de b, é dado por

(1,0) 2 - 

A London Eye é uma enorme roda-gigante na capital inglesa. Por ser um dos monumentos construídos para celebrar a entrada do terceiro milênio, ela também é conhecida como Roda do Milênio. Um turista brasileiro, em visita à Inglaterra, perguntou a um londrino o diâmetro (destacado na imagem) da Roda do Milênio e ele respondeu que ele tem 443 pés.

Não habituado com a unidade pé, e querendo satisfazer sua curiosidade, esse turista consultou um manual de unidades de medidas e constatou que 1 pé equivale a 12 polegadas, e que 1 polegada equivale a 2,54 cm. Após alguns cálculos de conversão, o turista ficou surpreendido com o resultado obtido em metros.

Qual a medida que mais se aproxima do diâmetro da Roda do Milênio, em metro?

(1,0) 3 - 

O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade v de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a) (v + b) = K, com a, b e K constantes.

Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:

O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p ; v). Admita que K > 0 .

Disponível em: http://rspb.royalsocietypublis.... Acesso em: 14 jul. 2015 (adaptado).

O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo

(1,0) 4 - 

Na figura estão representadas, em um plano cartesiano, duas circunferências: C₁ (de raio 3 e centro O₁) e C₂ (de raio 1 e centro O₂), tangentes entre si, e uma reta t tangente às duas circunferências nos pontos P e Q.

Nessas condições, a equação da reta t é

(1,0) 5 - 

Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.

A seguir há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.

Suponha que uma rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontre num ponto cujas coordenadas satisfaçam à inequação: x² + y² – 2x – 4y - 31 ≤ 0

A fim de avaliar a qualidade do sinal, e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio enquanto os outros não.

Os estabelecimentos que conseguem ouvir a rádio são apenas

(1,0) 6 - 

No jogo mostrado na figura, uma bolinha desloca-se somente de duas formas: ao longo de linhas retas ou por arcos de circunferências centradas no ponto O e raios variando de 1 a 8. Durante o jogo, a bolinha que estiver no ponto P deverá realizar a seguinte sequência de movimentos: 2 unidades no mesmo sentido utilizado para ir do ponto O até o ponto A e, no sentido anti-horário, um arco de circunferência cujo ângulo central é 120°.

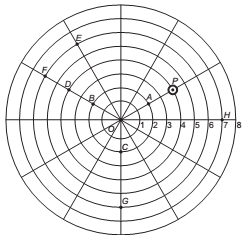
Após a sequência de movimentos descrita, a bolinha estará no ponto

(1,0) 7 - 

Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando “tiros”, seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0 ; 4), B(4 ; 4), C(4 ; 0), D(2 ; 2) e E(0 ; 2 ).

Passando pelo ponto A, qual equação fornecería a maior pontuação?

(1,0) 8 - 

No período de fim de ano, o síndico de um condomínio resolveu colocar, em um poste, uma iluminação natalina em formato de cone, lembrando uma árvore de Natal, conforme as figuras 1 e 2.

A árvore deverá ser feita colocando-se mangueiras de iluminação, consideradas segmentos de reta de mesmo comprimento, a partir de um ponto situado a 3 m de altura no poste até um ponto de uma circunferência de fixação, no chão, de tal forma que esta fique dividida em 20 arcos iguais. O poste está fixado no ponto C (centro da circunferência) perpendicularmente ao plano do chão.
Para economizar, ele utilizará mangueiras de iluminação aproveitadas de anos anteriores, que juntas totalizaram pouco mais de 100 m de comprimento, dos quais ele decide usar exatamente 100 m e deixar o restante como reserva.
Para que ele atinja seu objetivo, o raio, em metro, da circunferência deverá ser de

(1,0) 9 - 

Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.

A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade. No ponto P = (-5, 5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km.

Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto

(1,0) 10 - 

Observou-se que todas as formigas de um formigueiro trabalham de maneira ordeira e organizada. Foi feito um experimento com duas formigas e os resultados obtidos foram esboçados em um plano cartesiano no qual os eixos estão graduados em quilômetros. As duas formigas partiram juntas do ponto O, origem do plano cartesiano xOy. Uma delas caminhou horizontalmente para o lado direito, a uma velocidade de 4 km/h. A outra caminhou verticalmente para cima, à velocidade de 3 km/h.

Após 2 horas de movimento, quais as coordenadas cartesianas das posições de cada formiga?