Fração Geratriz: O que é e Como Calcular Dízimas Periódicas para Concursos

A Fração Geratriz é a representação fracionária exata de uma dízima periódica (aquele número decimal que possui repetição infinita). Como o nome sugere, essa fração é a "mãe" que gera a dízima quando seu numerador é dividido pelo denominador. Dominar a fração geratriz é um conhecimento essencial cobrado em concursos públicos e exames como o Enem. 🧠

Tecnicamente, a fração geratriz é um tipo de fração que, ao ser dividida, produz um número decimal não exato, pertencente ao conjunto dos números racionais ($\mathbb{Q}$). Ela é composta por:

• Parte Inteira: O número antes da vírgula.
• Período: O(s) algarismo(s) que se repete(m) infinitamente.
• Anteperíodo (em dízimas compostas): O(s) algarismo(s) que fica(m) entre a vírgula e o período.

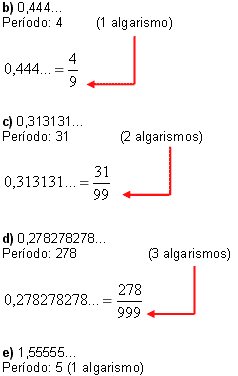
Veja alguns exemplos de fração geratriz e suas dízimas:

• $0,1111...$ (Período: 1)
• $1,3535...$ (Parte inteira: 1; Período: 35)
• $0,3177...$ (Anteperíodo: 31; Período: 7)
• $2,5555...$ (Parte inteira: 2; Período: 5)

VEJA TAMBÉM NO GUIA DA FRAÇÃO GERATRIZ

• Como se calcula a fração geratriz? (Método Algebrico)
• Fração geratriz: exercícios resolvidos passo a passo
• Fração geratriz calculadora (Exemplo Prático)
• Fração geratriz: como fazer pelo "Macete"
• Fração geratriz simples e composta
• Novos Simulados Enem
• Novas Questões Enem
• Provas Anteriores Enem

Como se calcula a fração geratriz? (Método Algebrico)

Para determinar a fração geratriz de uma dízima periódica, o método algébrico é o mais seguro e eficaz, especialmente para as dízimas periódicas compostas. Ele se baseia na criação de um sistema de equações simples.

Passos para encontrar a Fração Geratriz:

1. Igualar: Chame a dízima periódica de uma incógnita ($x$), formando a primeira equação ($x = 0,périodo...$).
2. Multiplicar (Parte 1): Multiplique a equação por potências de 10 até que o início do período passe para antes da vírgula.
3. Multiplicar (Parte 2): Multiplique a equação por potências de 10 até que um período inteiro passe para antes da vírgula.
4. Subtrair: Diminua a equação mais simples da equação mais complexa para eliminar as dízimas.
5. Isolar: Isole a incógnita ($x$) para encontrar a fração geratriz.

↑ voltar ao índice

Fração Geratriz: Exercícios Resolvidos Passo a Passo

Para fixar o conceito de dízima em fração e aprimorar sua Expertise, veja estes exemplos de fração geratriz aplicados a operações matemáticas:

Exercício I: Simplificando Operações com Dízimas

Utilizando a fração geratriz, encontre o resultado da seguinte operação:

3 . (1,0131313... – 0,0141414...)

Clique para ver a Resolução do Exercício I

O primeiro passo é transformar cada dízima em sua respectiva fração geratriz. Em seguida, subtrair e multiplicar por 3.

Exercício II: Soma de Dízimas Periódicas

Encontre a fração geratriz para realizar as seguintes operações entre números decimais:

a) $1,1212121212... + 1,17$

b) $23,012121212... + 1,14141414...$

Clique para ver a Resolução do Exercício II

Converta as dízimas em frações geratrizes e, em seguida, realize a soma de frações e números decimais.

↑ voltar ao índice

Fração Geratriz: Exemplo com Dízima Composta

Embora você possa usar uma calculadora de fração geratriz para conferir, é crucial saber o método manual para as provas. Veja o exemplo de uma dízima periódica composta:

Exemplo: Encontrando a geratriz de 0,37555...

Neste caso, o anteperíodo é $37$ (2 dígitos) e o período é $5$ (1 dígito).

• Numerador: (Anteperíodo seguido do Período) - (Anteperíodo) $\rightarrow 375 - 37 = 338$.
• Denominador: Um $9$ para cada dígito do período ($9$) + Dois $0$ para cada dígito do anteperíodo ($00$) $\rightarrow 900$.

Portanto, a fração geratriz inicial é:

$$\text{Fração Geratriz} = \frac{338}{900}$$

Como ambos os termos são divisíveis por 2, a fração geratriz irredutível é: $\frac{169}{450}$.

Essa fração irredutível $\frac{169}{450}$ é a geratriz da dízima $0,37555...$

↑ voltar ao índice

Fração Geratriz Simples: O Método Mais Rápido (Macete)

Para as dízimas periódicas simples (onde o período começa logo após a vírgula), existe um macete rápido para determinar a fração geratriz, evitando o cálculo algébrico demorado.

Exemplo: Fração geratriz de 0,8888...

• Num. Simples: O numerador é o período: $8$.
• Den. Simples: O denominador é formado por um $9$ para cada algarismo do período. Como o período tem apenas um algarismo ($8$), o denominador é $9$.

Assim, a fração geratriz é $\frac{8}{9}$:

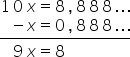
Pelo método algébrico:

$$10x - x = 8,888... - 0,888...$$$$9x = 8$$$$x = \frac{8}{9}$$

↑ voltar ao índice

Fração Geratriz Simples e Fração Geratriz Composta

Conhecer o tipo de dízima é crucial para aplicar o método correto e se sair bem nas questões de Matemática para concursos.

1. Fração Geratriz Simples (Dízima Periódica Simples)

Ocorre quando o período se inicia imediatamente após a vírgula. Ex: $0,484848...$ ou $5,333...$

• Macete: O numerador é o período, e o denominador é formado apenas por $9$'s (um $9$ para cada algarismo do período).

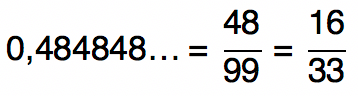
Lembrete: Sempre que possível, simplificar a fração geratriz encontrada até torná-la irredutível.

2. Fração Geratriz Composta (Dízima Periódica Composta)

Ocorre quando existe um ou mais algarismos (o anteperíodo) entre a vírgula e o período. Ex: $0,15444...$ ou $2,37555...$

• Macete: O numerador é (Anteperíodo + Período) - (Anteperíodo). O denominador é formado por $9$'s (período) seguido de $0$'s (anteperíodo).

↑ voltar ao índice

---

Dúvidas Frequentes sobre Fração Geratriz (FAQ)

O que é a Fração Geratriz?

A Fração Geratriz é a fração que, por meio de sua divisão (numerador pelo denominador), origina uma dízima periódica, que é um número decimal com repetição infinita de algarismos.

Toda dízima periódica tem uma fração geratriz?

Sim. Como toda dízima periódica é um número racional, ela pode ser expressa obrigatoriamente como uma fração geratriz, ou seja, uma razão entre dois números inteiros.

Para que serve a Fração Geratriz em provas?

Em concursos, o conhecimento da fração geratriz é necessário para resolver operações matemáticas (adição, subtração, multiplicação) que envolvam dízimas periódicas, garantindo um resultado exato.

Qual a diferença entre Fração Geratriz Simples e Composta?

Na Simples, o período começa logo após a vírgula. Na Composta, existe um algarismo ou grupo de algarismos (o anteperíodo) entre a vírgula e o período.

---

Domine a Fração Geratriz com Simulados!

A melhor forma de memorizar as fórmulas da geratriz é praticando. O ConcursosAZ oferece milhares de questões de Matemática cobradas em concursos e no Enem para você aplicar o que aprendeu.

↑ voltar ao índice